Game Theory

Game theory is a mathematical theory that studies the interaction behavior among decision-makers. In game theory, decision-makers, known as "players", make choices (strategies) according to rules (the form of the game) and obtain certain outcomes (payoffs or utilities) based on the choices of all players. Game theory covers the rationality assumptions of players, players' expectations, and players' strategy choices. Game theory can be divided into cooperative and non-cooperative games. Cooperative games focus on teamwork and the formation of alliances, with a particular emphasis on how to distribute payoffs. Non-cooperative games presume that players will selfishly pursue their interests, with the classic example being the prisoner's dilemma.

There are a large number of gaming application scenarios in blockchain

1. Voting or Election: Consensus mechanisms in blockchain include forms of election or voting, such as which block to add next or deciding the truthful chain in case of forks. Game theory provides a model to understand the strategic interactions and potential behaviors of participants in these decisions.
2. Auctions: Auctions, as in the case of token sales or gas fees bidding in Ethereum, play a significant role in blockchain. A strategic analysis using game theory can optimize the auction designs and predict bidding behaviors, potentially increasing the overall efficiency of such systems.
3. DeFi (Decentralized Finance) Models: Complex mechanisms like Miner Extractable Value (MEV) and models like Ve(3,3) in Curve Finance are analyzed using game theory. It helps understand how rational users behave in various market conditions, considering different incentives provided by these models.

Nash Equilibrium

Nash equilibrium is a significant concept in game theory, introduced by mathematician John Nash in 1950, which describes a stable state of a game. In this state, each player selects the optimal strategy according to the strategies of all other players, and under the premise of knowing all other players' choices, no player can increase their own payoffs by unilaterally changing strategies. Simply put, a Nash equilibrium is the intersection of each player's best responses - when the game reaches a Nash equilibrium, no player wants to change their strategy. While Nash equilibrium provides a theoretical framework to understand how decision-makers make rational choices, there are relatively few examples in reality that can reach a Nash equilibrium. This is mainly because players' rational selections can be influenced by various factors, such as limited information and bounded rationality. Nevertheless, Nash equilibrium remains an important tool for understanding and analyzing strategic decision interactions.

Perfect Information Games vs Imperfect Information Games

Perfect Information Games

In games of perfect information, every player has complete knowledge about the game and the actions of other players. That is, each player is aware of all the previous moves made by all the players. Classic examples of such games are chess and go, where each player observes the entire history of the game and can make the optimal decision at each step. In the context of blockchain, perfect information might apply to consensus mechanisms where the actions of all validators are transparent and open to the network, such as Proof-of-Work or a public ledger’s transaction history.

In games of perfect information, a Nash equilibrium represents a state of the game where no player can unilaterally deviate from their current strategy to improve their payoff, given the strategies of all other players. The process of finding a Nash equilibrium in such games is relatively straightforward because all players have complete knowledge about the game structure and the past actions of all players. The concept of Nash equilibrium in this setting aligns with the idea of strategy profiles that are stable under mutual best response dynamics.

Imperfect Information Games

Contrastingly, in games of imperfect information, some aspects of the game are not fully known to all players. Players may have private knowledge or there may be uncertainty about the past actions of other players. This can lead to strategic behavior where players infer from incomplete information or signal to other players. Poker is an example of such a game, where each player does not know the cards that others hold. In blockchain applications, imperfect information often arises. An example would be a privacy-preserving blockchain where transaction data is hidden, or in peer-to-peer trading where one does not know the reservation price of a counterparty.

In games of imperfect information, a Nash equilibrium is a more complex concept. It's still defined as a state of the game where no player can profit from unilaterally deviating from their current strategy, given the strategies of others. However, because players now have private information, a player's strategy must specify what to do for every possible private information they can have. The Nash equilibrium concept in this case extends to the notion of a Bayesian Nash equilibrium, which considers players' beliefs about each other's private information, and each player's strategy is the best response to their beliefs about others' strategies. Therefore, in imperfect information games, Nash equilibria can involve complex strategic behavior like randomization (mixing between different actions) and sophisticated beliefs about others' private information.

In summary, while the basic intuition of Nash equilibrium - no profitable unilateral deviation - applies in both perfect and imperfect information games, the nature of strategies and the process to derive equilibria can be significantly more complex in games of imperfect information.

An example in Ve(3,3)

A very typical example is the Ve(3,3) model proposed by OHM.

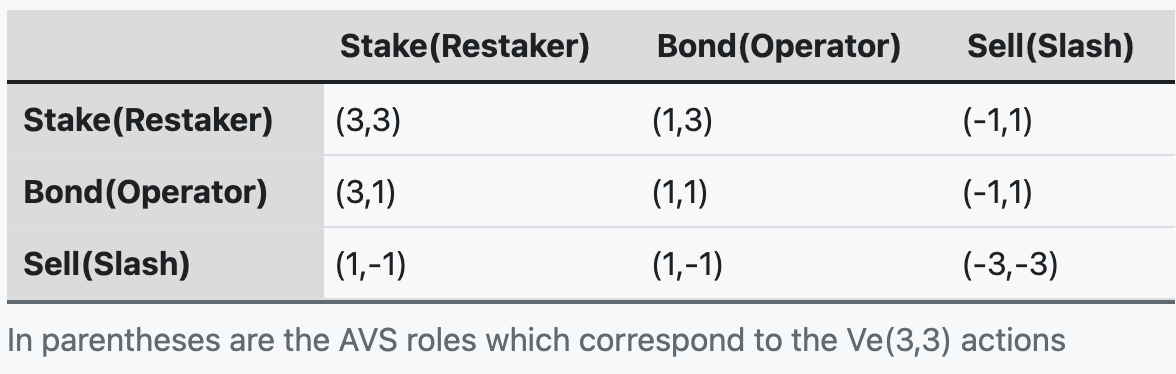
The Nash equilibrium of this game model is located at point (3,3), which in turn, allows the maximization of the Total Value Locked (TVL) for the whole ecosystem. Within just five months, the TVL of OHM rapidly escalated to $800M. Nonetheless, due to the inherent data transparency of the blockchain, this game is one of perfect information, meaning that all participants know each other's information. As such, this game only reaches Nash equilibrium briefly. The reason is that once you are aware of other participants starting to exit the system, you, too, would leave the game.

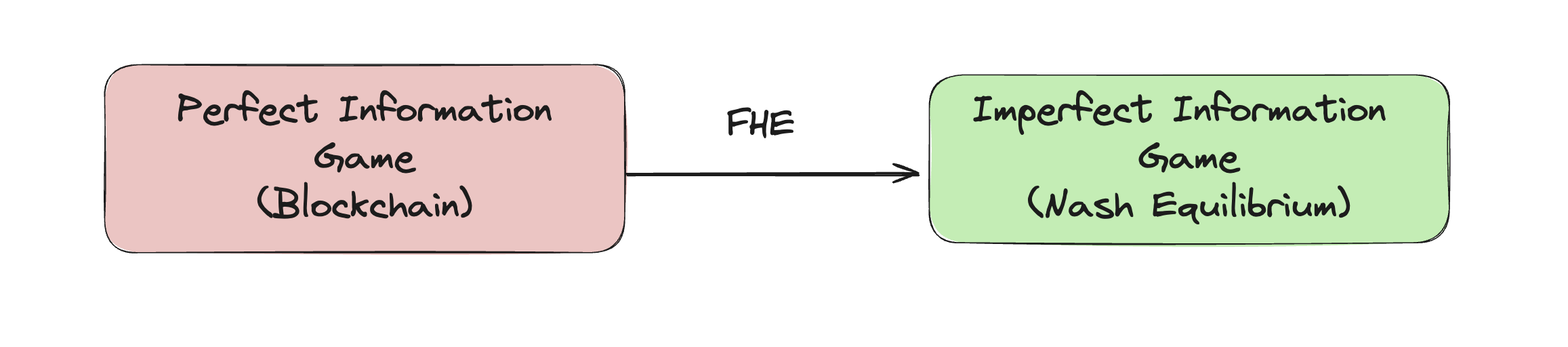
With the help of Fully Homomorphic Encryption (FHE), we can transform the perfect information game into an imperfect information game, thereby achieving the Nash equilibrium point.